10. Sınıf Matematik Konuları Ve Müfredatı MEB (2022-2023)

2022 ve 2023 10. Sınıf Matematik Konuları ve Müfredatı MEB. Lise 10. Sınıf Matematik konuları ve Müfredatı nelerdir? 10. Sınıf Matematik Müfredatı 2022-2023. Lise 10. Sınıf Matematik ders içerikleri ve detayları yazımızda.

10. Sınıf Matematik Konuları

2022 ve 2023 Eğitim Öğretim Yılı MEB 10. Sınıf Matematik konuları ve müfredatı belli oldu!. Lise 10. Sınıf Matematik Konuları ve Müfredatı OLASILIK, FONKSİYONLAR, İKİNCİ DERECEDEN DENKLEMLER, DÖRTGENLER VE ÇOKGENLER gibi konulardan oluşmaktadır. 10. Sınıf Matematik dersinde işlenecek konular iki dönem halinde aşağıda paylaşıldı. 2022 ve 2023 10.Sınıf Matematik Konuları ve Müfredatı şu şekildedir;

10. Sınıf Matematik Konuları 1.Dönem

• 10. Sınıf Matematik Konuları
• 1. ÜNİTE: Sayma ve Olasılık
  • Sıralama ve Seçme
  • Permütasyon
  • Kombinasyon
  • Pascal Üçgeni
  • Binom Açılımı
  • Basit Olayların Olasılıkları
• 2. ÜNİTE: Fonksiyonlar
  • Fonksiyon Kavramı ve Gösterimi
  • Fonksiyonlar
  • Fonksiyon Grafikleri
  • Doğrusal Fonksiyonlar
  • İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi
  • Birebir ve Örten Fonksiyon
  • Bileşke Fonksiyon
  • Bir Fonksiyonun Tersi
• 3. ÜNİTE: Polinomlar
  • Polinom Kavramı
  • Polinomlarda İşlemler
  • Polinomların Çarpanlara Ayrılması
  • Polinomlarda Sadeleştirme

TYT AYT TESTLERİ ÇÖZ

10. Sınıf Matematik Konuları 2.Dönem

• 10. Sınıf Matematik Konuları
• 4. ÜNİTE: İkinci Dereceden Denklemler
  • İkinci Derecen Bir Bilinmeyenli Denklemler
  • Karmaşık Sayılar
  • İkinci Dereceden Bir Bilinmeyenleri Denklemlerin Kökleri ve Katsayıları
• 5. ÜNİTE: Dörtgenler ve Çokgenler
  • Çokgenler
  • Çokgen ve Temel Elemanları
  • Düzgün Çokgenler
  • Dörtgenler ve Özellikleri
  • Dörtgenler
  • Yamuk
  • Paralelkenar
  • Eşkenar Dörtgen
  • Dikdörtgen
  • Kare
  • Deltoid
• 6. ÜNİTE: Uzay Geometri
  • Katı Cisimler
  • Dik Prizmalar
  • Dik Piramitler

10. SINIF DERS KİTAPLARI

10. SINIF KONULARI MEB

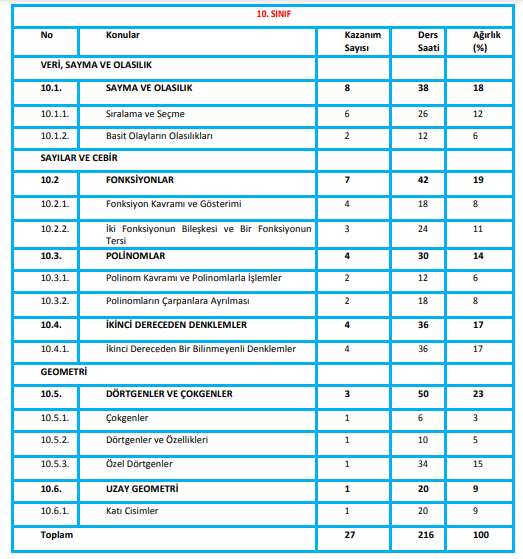
10. Sınıf Matematik Dersi Kazanımları

10. Sınıf Matematik Konuları ve Kazanımları aşağıdadır.

10. SINIF ALT ÖĞRENME ALANI, KONU, KAZANIM VE AÇIKLAMALARI

VERİ, SAYMA VE OLASILIK
10.1. Sayma ve Olasılık
10.1.1. Sıralama ve Seçme
Terimler ve Kavramlar: toplama yöntemi, çarpma yöntemi, faktöriyel, permütasyon, tekrarlı permütasyon, kombinasyon, Pascal üçgeni, binom açılımı, Sembol ve Gösterimler: ?! , ?(?, ?) , ?(?, ?)

10.1.1.1. Olayların gerçekleşme sayısını toplama ve çarpma yöntemlerini kullanarak hesaplar.
a) Sayma konusunun tarihsel gelişim sürecinden söz edilir ve bu süreçte rol alan Sâbit İbn Kurrâ‘nın çalışmalarına yer verilir.
b) Faktöriyel kavramı verilerek saymanın temel ilkesi ile ilişkilendirilir.
10.1.1.2. n çeşit nesne ile oluşturulabilecek r li dizilişlerin (permütasyonların) kaç farklı şekilde yapılabileceğini hesaplar.
10.1.1.3. Sınırlı sayıda tekrarlayan nesnelerin dizilişlerini (permütasyonlarını) açıklayarak problemler çözer.
a) En az iki tanesi özdeş olan nesnelerin tüm farklı dizilişlerinin sayısı örnekler/problemler bağlamında ele alınır.
b) Gerçek hayat problemlerine yer verilir.
10.1.1.4. n elemanlı bir kümenin r tane elemanının kaç farklı şekilde seçilebileceğini hesaplar.
a) Kombinasyon kavramı alt küme sayısı ile ilişkilendirilir.

b) Kombinasyon kavramının aşağıdaki temel özellikleri incelenir:
• ??(?, ?) = ?(?, ? − ?)
• ?(?, 0) + ?(?, 1) + ⋯ + ?(?, ?) = 2ⁿ

0.1.1.5. Pascal üçgenini açıklar.
Pascal üçgeninin, aralarında Ömer Hayyam’ın da bulunduğu Hint, Çin, İslam medeniyetlerindeki matematikçi ve düşünürler tarafından Pascal’dan çok önceleri ele alındığı; bu çerçevede matematiksel bilginin oluşumunda farklı kültür ve bilim insanlarının rolü vurgulanır.
10.1.1.6. Binom açılımını yapar.
a) Binom açılımı Pascal üçgeni ile ilişkilendirilir.
b) Sadece iki terimli ifadelerin açılımı ele alınır.
c) Binom formülü ile ilgili örnekler yapılır ancak (???? + ????)?? açılımında ? ∈ ℕ, ?, ? ∈ ℚ′ şeklindeki
örneklere yer verilmez.

10.1.2. Basit Olayların Olasılıkları
Terimler ve Kavramlar: örnek uzay, olay, deney, çıktı, kesin olay, imkânsız olay, ayrık olay, ayrık olmayan olay, bir olayın tümleyeni, olasılık. Sembol ve Gösterimler: E, P(A), P(A’)
10.1.2.1. Örnek uzay, deney, çıktı, bir olayın tümleyeni, kesin olay, imkânsız olay, ayrık olay ve ayrık olmayan olay kavramlarını açıklar.
a) Örnek uzay, deney, çıktı kavramları eş olası durumlardan yola çıkılarak eş olası olmayan durumlar için de örneklendirilir ve tanımlanır.
b) Ayrık olay ve ayrık olmayan olay üzerinde durulur.

c) El Kindî ve Laplace’ın çalışmalarına yer verilir.
10.1.2.2. Olasılık kavramı ile ilgili uygulamalar yapar.
a) Eş olası olan ve olmayan olayların olasılıkları hesaplanır.
b) Tümleyen, ayrık olay ve ayrık olmayan olay ile ilgili olasılıklar hesaplanır.
c) Gerçek hayat problemlerine yer verilir

SAYILAR VE CEBİR
10.2. Fonksiyonlar
10.2.1. Fonksiyon Kavramı ve Gösterimi
Terimler ve Kavramlar: fonksiyon, tanım kümesi, değer kümesi, görüntü kümesi, fonksiyonun grafiği, sabit
fonksiyon, içine fonksiyon, örten fonksiyon, bire bir fonksiyon, eşit fonksiyon, birim fonksiyon, doğrusal
fonksiyon, tek fonksiyon, çift fonksiyon, dikey (düşey) doğru testi
Sembol ve Gösterimler: ?: ? → ?, ?(?), ? = ?(?), ? + ?, ? − ?, ?. ?, ?/? , ?

10.2.1.1. Fonksiyonlarla ilgili problemler çözer.
a) Fonksiyon kavramı açıklanır.
b) Sadece gerçek sayılar üzerinde tanımlanmış fonksiyonlar ele alınır.
c) İçine fonksiyon, örten fonksiyon, bire bir fonksiyon, eşit fonksiyon, birim (özdeşlik) fonksiyon, sabit
fonksiyon, doğrusal fonksiyon, tek fonksiyon, çift fonksiyon ve parçalı tanımlı fonksiyon açıklanır.
ç) İki fonksiyonun eşitliği örneklerle açıklanır.
d) f ve g fonksiyonları kullanılarak ? + ?, ? − ?, ?. ?, ?/? işlemleri yapılır, ancak parçalı tanımlı fonksiyonlarda bu işlemlere girilmez.

e) Gerçek hayat problemlerine ve tablo-grafik kullanımına yer verilir.
10.2.1.2. Fonksiyonların grafiklerini çizer.
a) f(x) = ax + b şeklindeki fonksiyonların grafikleri ile ilgili uygulamalar yapılır.
b) Parçalı tanımlı şekilde verilen fonksiyonların grafikleri çizilir.

c) f(x) = ax + b tipindeki fonksiyonların grafiği bilgi ve iletişim teknolojileri yardımıyla çizilerek a ve b katsayıları ile fonksiyon grafiği arasındaki ilişki ele alınır.
10.2.1.3. Fonksiyonların grafiklerini yorumlar.

a) Grafiği verilen fonksiyonların tanım ve görüntü kümeleri gösterilir.
b) Bir fonksiyon grafiğinde, fonksiyonun x ekseni üzerinde tanımlı olduğu her bir noktadan y eksenine
paralel çizilen doğruların, grafiği yalnızca bir noktada kestiğine (düşey/dikey doğru testi) işaret edilir.
c) Bir f fonksiyonunun grafiğinin y = f(x) denkleminin grafiği olduğu ve grafiğin (varsa), x eksenini kestiği
noktaların f(x) = 0 denkleminin gerçek sayılardaki çözüm kümesi olduğu vurgulanır.
10.2.1.4. Gerçek hayat durumlarından doğrusal fonksiyonlarla ifade edilebilenlerin grafik gösterimlerini
yapar.

10.2.2. İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi
Terimler ve Kavramlar: bileşke fonksiyon, fonksiyonun tersi, yatay doğru testi
Sembol ve Gösterimler: ???, ?−1
10.2.2.1. Bire bir ve örten fonksiyonlar ile ilgili uygulamalar yapar.
a) Bir fonksiyonun bire bir ve örtenliği grafik üzerinde yatay doğru testiyle incelenir ve cebirsel olarak
ilişkilendirilir.

b) Bilgi ve iletişim teknolojileri yardımıyla bir fonksiyonun bire bir ve örten olup olmadığı belirlenir.
10.2.2.2. Fonksiyonlarda bileşke işlemiyle ilgili işlemler yapar.
a) Bileşke işlemi, fonksiyonların cebirsel ve grafik gösterimleri ile ilişkilendirilerek ele alınır.
b) Fonksiyonlarda bileşke işleminin birleşme özelliğinin olduğu belirtilir, değişme özelliğinin olmadığı
örneklerle gösterilir.

c) Parçalı tanımlı fonksiyonların bileşkesine girilmez.
10.2.2.3. Verilen bir fonksiyonun tersini bulur.
a) Bir fonksiyonun tersinin de fonksiyon olması için gerekli şartlar belirtilir.
b) Sadece bire bir ve örten doğrusal fonksiyonun tersinin grafiği çizilir; fonksiyonun grafiği ile tersinin grafiğinin y=x doğrusuna göre simetrik olduğu gösterilir.
c) Parçalı tanımlı fonksiyonların tersi verilmez.

10.3. Polinomlar
10.3.1. Polinom Kavramı ve Polinomlarla İşlemler
Terimler ve Kavramlar: polinom, polinomun derecesi, polinomun katsayıları, polinomun baş katsayısı,
polinomun sabit terimi, sabit polinom, sıfır polinomu, polinomun sıfırları
Sembol ve Gösterimler: P(x)
10.3.1.1. Bir değişkenli polinom kavramını açıklar.
a) Polinomun derecesi, katsayıları ve sabit terimi belirtilir.
b) Sabit polinom, sıfır polinomu ve iki polinomun eşitliği örneklerle açıklanır

10.3.1.2. Polinomlarla toplama, çıkarma, çarpma ve bölme işlemlerini yapar.
a) Bir P(x) polinomunun x – a ile bölümünden kalan P(a) dır.
?(?) = 0 ⇔ ? – ?, ?(?) in bir çarpanı olduğu vurgulanır.
b) Polinomun sıfırı kavramı bölme işlemiyle ilişkilendirilir.

10.3.2. Polinomların Çarpanlara Ayrılması
Terimler ve Kavramlar: çarpan, özdeşlik, değişken değiştirme, rasyonel ifade
10.3.2.1. Bir polinomu çarpanlarına ayırır.
a) Ortak çarpan parantezine alma ve değişken değiştirme yöntemleri kullanılarak çarpanlara ayırma
uygulamaları yapılır.
b) Tam kare, iki kare farkı, iki terimin toplamının ve farkının küpü, iki terimin küplerinin toplamı ve farkına
ait özdeşlikler kullanılarak çarpanlara ayırma uygulamaları yapılır.
c) ?x² + ?x+ ? biçimindeki ifadeler çarpanlarına ayrılır.

10.3.2.2. Rasyonel ifadelerin sadeleştirilmesi ile ilgili işlemler yapar.
a) Rasyonel ifade kavramı tanıtılır.
b) Çarpanları polinom olmayan ifadelerde çarpanlara ayırma uygulamalarına yer verilmez.

10.4. İkinci Dereceden Denklemler
10.4.1. İkinci Dereceden Bir Bilinmeyenli Denklemler
Terimler ve Kavramlar: ikinci dereceden bir bilinmeyenli denklem, denklemin kökü, kökler toplamı, kökler
çarpımı, diskriminant, karmaşık sayı, eşlenik
Sembol ve Gösterimler: Δ, i, a+ib, z, Ȼ, İm(z), Re(z)

10.4.1.1. İkinci dereceden bir bilinmeyenli denklem kavramını açıklar.
İkinci dereceden bir bilinmeyenli denklemlerin tarihsel gelişim sürecine ve bu süreçte rol alan Brahmagupta,
Harezmî ve Abdulhamid İbn Türk’ün çalışmalarına yer verilir.

10.4.1.2. İkinci dereceden bir bilinmeyenli denklemleri çözer.
a) ax2 + bx + c biçimindeki cebirsel ifadelerin; tam kare ve iki kare farkına ait özdeşlikler kullanılarak
çarpanlara ayrılmasıyla ilgili uygulamalar yapılır.
b) Denklemlerin çözümünde farklı yöntemlerden (çarpanlara ayırma, tam kareye tamamlama, değişken
değiştirme, iki kare farkı, diskriminant) yararlanılır.

c) Gerçek hayat problemlerine yer verilir.
10.4.1.3. Bir karmaşık sayının a+ib (a,b ∈ ℝ) biçiminde ifade edildiğini açıklar.
a)Diskriminantın sıfırdan küçük olduğu durumlarda ikinci dereceden bir bilinmeyenli denklemlerin
köklerinin bulunabilmesi için gerçek sayılar kümesini kapsayan yeni bir sayı kümesi tanımlama gereği
örneklerle açıklanır.
b) ?²= −1 olmak üzere bir karmaşık sayı ?+?b(?, ? ∈ ℝ) biçiminde gösterilir.
c) Köklerin birbirinin eşleniği olduğu belirtilir.

ç) Karmaşık sayının eşleniği dışındaki özelliklere ve işlemlere girilmez.
10.4.1.4. İkinci dereceden bir bilinmeyenli denklemin kökleri ile katsayıları arasındaki ilişkileri
kullanarak işlemler yapar.
a) Sadece kökler toplamı ve çarpımı ile denklemin katsayıları arasındaki ilişkiler üzerinde durulur.
b) Kökleri verilen ikinci dereceden denklemi elde etme ile ilgili uygulamalara yer verilir.

GEOMETRİ
10.5. Dörtgenler ve Çokgenler
10.5.1. Çokgenler
Terimler ve Kavramlar: çokgen, düzgün çokgen, köşegen
10.5.1.1. Çokgen kavramını açıklayarak işlemler yapar.
a) İçbükey çokgenlere girilmez.
b) Düzgün çokgenler hatırlatılır, iç ve dış açılarının ölçüleri bulunur.
c) Çokgenlerin köşegenleri ile ilgili özelliklere ve alan problemlerine yer verilmez.
10.5.2. Dörtgenler ve Özellikleri
Terimler ve Kavramlar: dışbükey dörtgen, içbükey dörtgen, köşegen, çevre, alan
Sembol ve Gösterimler: Ç(ABCD), A(ABCD)

10.5.2.1. Dörtgenin temel elemanlarını ve özelliklerini açıklayarak problemler çözer.
a) Dışbükey ve içbükey dörtgen kavramları açıklanır. (Bundan sonra dörtgen denildiğinde dış bükey
dörtgen anlaşılmalıdır.)
b) Dörtgenin iç ve dış açılarının ölçüleri toplamı bulunur.
c) Dörtgenin çevresi üzerinde durulur.

10.5.3. Özel Dörtgenler
Terimler ve Kavramlar: yamuk, ikizkenar yamuk, dik yamuk, paralelkenar, eşkenar dörtgen, dikdörtgen,
kare, deltoid
10.5.3.1. Özel dörtgenlerin açı, kenar, köşegen ve alan özelliklerini açıklayarak problemler çözer.
a) Yamuk, paralelkenar, eşkenar dörtgen, dikdörtgen, kare ve deltoid arasındaki hiyerarşik ilişkilere yer
verilir.

b) Hiyerarşik ilişkiye göre her bir özel dörtgen kendi içerisinde; açı, kenar, köşegen ve alan özellikleri
bağlamında ele alınır.
c) Origami, tangram kullanılarak uygulamalar yapılır.
ç) Geleneksel mimaride kullanılan motif örneklerinde yer alan çokgen örneklerine yer verilir.
d) Bilgi ve iletişim teknolojilerinden yararlanılır.

10.6. Uzay Geometri
10.6.1. Katı Cisimler
Terimler ve Kavramlar: dik prizma, dik piramit, yükseklik, taban alanı, yüzey alanı, yanal alan, hacim
10.6.1.1. Dik prizmalar ve dik piramitlerin uzunluk, alan ve hacim bağıntılarını oluşturur.
a) Üçgen, dörtgen ve altıgen dik prizma/piramit ile sınırlandırılır.
b) Gerçek hayat problemlerine yer verilir.
c) Bilgi ve iletişim teknolojilerinden yararlanılır

10. Sınıf Matematik Konuları ve Müfredatı MEB (2022-2023). Milli Eğitim Bakanlığı (MEB) müfredatına uyumlu olarak hazırlanan 10. Sınıf Matematik konuları yukarıda listelenmiştir. 10. Sınıf Matematik Konuları tüm yıl boyunca işlenmektedir. Konulara ait testleri ve 10. Sınıf PDF ders kitaplarını sitemizde bulabilirsiniz. 10. Sınıf Matematik Testleri sitemizde paylaşıldı. 10. Sınıf Tüm Matematik testlerini çözmek için TIKLA

10. SINIF TEKRAR TESTLERİ

TYT AYT DENEME SINAVLARI PDF

Bunlara da Bakabilirsiniz!

• 10. Sınıf Konuları MEB
• 10. Sınıf Ders Kitapları
• 10. Sınıf Tekrar Testleri
• TYT AYT Konuları MEB
• TYT AYT Deneme Sınavları
• TYT AYT Örnek Sorular
• TYT Kaç Net Kaç Puan
• MEB Kazanım Testleri
• Beceri Temelli Sorular
• Haftalık Ders Çizelgesi
• MEB Çalışma Fasikülleri
• 10. Sınıf Müfredatı